DISTRIBUCIONES.

DISTRIBUCION NORMAL

En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece aproximada en fenómenos reales.

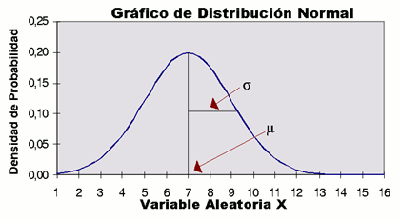
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.

La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.

De hecho, la estadística es un modelo matemático que sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.

La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.

Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:

• caracteres morfológicos de individuos como la estatura;
• caracteres fisiológicos como el efecto de un fármaco;
• caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos;
• caracteres psicológicos como el cociente intelectual;
• nivel de ruido en telecomunicaciones;
• errores cometidos al medir ciertas magnitudes;
• etc.

La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.^[] Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una supuesta "normalidad".

En probabilidad, la distribución normal aparece como el límite de varias distribuciones de probabilidad continuas y discretas.

Distribución normal
La línea verde corresponde a la distribución normal estándar Función de densidad de probabilidad
Función de distribución de probabilidad
Parámetros
Dominio
Función de densidad (pdf)
Función de distribución (cdf)
Media
Mediana
Moda
Varianza
Coeficiente de simetría	0
Curtosis	0
Entropía
Función generadora de momentos (mgf)
Función característica

TEOREMA DE LA COMBINACIÓN LINEAL DE VARIACIONES NORMALES Y CHI-CUADRADAS.

Terorema de Chebshev, este teorema da una estimación conservadora de la probabilidad de que una variable aleatoria tome un valor dentro de k dentro de k desviaciones estándar de su media para cualquier número real k. Proporcionaremos solo la demostración para caso continuo.

La probabilidad de que cualquier variable aleatoria X tome un valor dentro de k desviaciones estándar de la media es al menos 1-. Es decir

DISTRIBUCIONES MUÉSTRALES.

Las muestras aleatorias obtenidas de una población son, por naturaleza propia, impredecibles. No se esperaría que dos muestras aleatorias del mismo tamaño y tomadas de la misma población tenga la misma media muestral o que sean completamente parecidas; puede esperarse que cualquier estadístico, como la media muestral, calculado a partir de las medias en una muestra aleatoria, cambie su valor de una muestra a otra, por ello, se quiere estudiar la distribución de todos los valores posibles de un estadístico. Tales distribuciones serán muy importantes en el estudio de la estadística inferencial, porque las inferencias sobre las poblaciones se harán usando estadísticas muestrales. Como el análisis de las distribuciones asociadas con los estadísticos muestrales, podremos juzgar la confiabilidad de un estadístico muestral como un instrumento para hacer inferencias sobre un parámetro poblacional desconocido.

Como los valores de un estadístico, tal como x, varían de una muestra aleatoria a otra, se le puede considerar como una variable aleatoria con su correspondiente distribución de frecuencias.

La distribución de frecuencia de un estadístico muestral se denomina distribución muestral. En general, la distribución muestral de un estadístico es la de todos sus valores posibles calculados a partir de muestras del mismo tamaño.

Suponga que se han seleccionado muestras aleatorias de tamaño 20 en una población grande. Se calcula la madia muestral x para cada muestra; la colección de todas estas medias muestrales recibe el nombre de distribución muestral de medias, lo que se puede ilustrar en la siguiente figura:

Suponga que se eligen muestras aleatorias de tamaño 20, de una población grande, y se calcula la deviación estándar de cada una. La colección de todas estas desviaciones estándar muestrales se llama distribución muestral de la desviación estándar, y lo podemos ver en la siguiente figura:

Ejemplo 1.6

Se eligen muestras ordenadas de tamaño 2, con reemplazo, de la población de valores 0, 2, 4 y 6. Encuentre:

, la media poblaciona.

, la desviación estándar poblacional.

_x, la media de la distribución muestral de medias.

_x, la desviación estándar de la distribución muestral de medias.

Además, grafique las frecuencias para la población y para la distribución muestral de medias.

Solución:

1. La media poblacional es:

1. 
   
   
2. La desviación estándar de la población es:
3. 
   
4. A continuación se listan los elementos de la distribución muestral de la media y la correspondiente distribución de frecuencias.

La media de la distribución muestral de medias es:

d) La desviación estándar de la distribución muestral de medias es:

De aquí que podamos deducir que:

Como para cualquier variable aleatoria, la dsitribución muestral de medias tiene una media o valor esperado, una varianza y una desviación estándar, se puede demostrar que la distribución muestral de medias tiene una media igual a la media poblacional. Esto es:

Distribuciones muestrales

Después de haber realizado el ejercicio anterior se puede ver que una distribución muestral se genera extrayendo todas las posibles muestras del mismo tamaño de la población y calculándoles a éstas su estadístico.

Si la población de la que se extraen las muestras es normal, la distribución muestral de medias será normal sin importar el tamaño de la muestra.

Si la población de donde se extraen las muestras no es normal, entonces el tamaño de la muestra debe ser mayor o igual a 30, para que la distribución muestral tenga una forma acampanada. Mientras mayor sea el tamaño de la muestra, más cerca estará la distribución muestral de ser normal.

Para muchos propósitos, la aproximación normal se considera buena si se cumple n=30. La forma de la disitribución muestral de medias sea aproximadamente normal, aún en casos donde la población original es bimodal, es realmente notable.

                                             DISTRIBUCIONES. T.

En la generalidad de los casos, no disponemos de la desviación standard de la población, sino de una estimación calculada a partir de una muestra extraída de la misma y por lo tanto no podemos calcular Z.
En estos casos calculamos el estadístico T: T=μ−xs con s=∑(x−xi)2n−1−−−−−−−−−−√
donde S es la desviación standard muestral, calculada con n-1 grados de libertad. Nótese que utilizamos S, la Desviación Standard de una Muestra, en lugar de μ, la Desviación Standard de la Población. El estadístico T tiene una distribución que se denomina distribución T de Student, que está tabulada para 1, 2, 3, ... etc. grados de libertad de la muestra con la cual se calculó la desviación standard. La distribución T tiene en cuenta la incertidumbre en la estimación de la desviación standard de la población, porque en realidad la tabla de T contiene las distribuciones de probabilidades para distintos grados de libertad. La distribución T es mas ancha que la distribución normal tipificada Para un número de grados de libertad pequeño. Cuando los grados de libertad tienden a infinito, la distribución T tiende a coincidir con la distribución normal standard. Es decir, en la medida que aumentemos el número de observaciones de la muestra, la desviación standard calculada estará mas próxima a la desviación standard de la población y entonces la distribución T correspondiente se acerca a la distribución normal standard. El uso de la distribución T presupone que la población con que estamos trabajando tiene una distribución normal. Distribución de Promedios Muestrales Para comprender que significa distribución de promedios muestrales, vamos a suponer que realizamos un experimento con bombos como los usados en la lotería. Colocamos un número muy grande de bolas blancas en un bombo blanco, en cada una de las cuales figura un dato X. Este bombo representa la población de observaciones X, y tiene media m y varianza s2. Supongamos que a continuación hacemos los siguiente: 1) Tomamos una muestra de n=10 bolas blancas. 2) Calculamos la media y la anotamos en una bola azul. 3) Colocamos la bola azul en un segundo bombo de color azul. 4) Devolvemos las bolas blancas a su bombo y le damos vueltas. 5)Repetimos toda la operación muchas veces hasta que el bombo azul esté lleno de bolas azules. Entonces, los números del bombo azul forman una población de promedios muestrales. Esta es una población derivada de la anterior, y tiene la misma media o promedio que la distribución original, pero su varianza es un enésimo de la varianza de la distribución original: V(X−−)=σ2n En el caso del bombo azul, si denominamos σ2m a la varianza y μm a la media, tenemos: μm=μyσ2m=σ210 La distribución de medias muestrales está situada en el mismo lugar (alrededor de la misma media) que la distribución original, pero es mucho mas estrecha, porque su varianza es la décima parte de la varianza original. La distribución original de observaciones representada por el bombo blanco se denomina comúnmente distribución madre o base. Al construir la población de promedios muestrales, realizábamos extracciones de 10 bolas blancas después de dar vueltas al bombo. Es decir, que estábamos realizando un muestreo aleatorio de la población madre, porque cada una de las bolas blancas tenía la misma posibilidad de ser elegida para integrar la muestra. Aunque la población original no sea de distribución normal, si el muestreo es aleatorio, la población de promedios muestrales se aproximará a la normalidad, es decir, será casi de distribución normal. Este efecto se debe a un teorema de estadística matemática denominado Teorema Central del Límite. En resumen, si se cumple la hipótesis de muestreo aleatorio, tenemos: mediaVarianzaDesv. StandardForma de la curvadistribucion de xms2scualquieradistribucion de x¯mσ2/nσ/n√mascercadelanormal En general, en los problemas que se presentan habitualmente, existe una población de observaciones cualesquiera, de la cual tomamos una muestra aleatoria, por medio de la cual intentamos conocer todo lo que sea posible acerca de la población de la cual fue extraída. El promedio de la muestra de n elementos pertenece a la distribución de promedios muestrales de la población original. Es decir, que el promedio de la muestra que obtuvimos es uno de los muchos promedios muestrales que se distribuyen alrededor de m con desviación standard. Por lo tanto, si la muestra es mas grande (n mayor), estaremos en una distribución de promedios con desviación standard mas pequeña, por lo cual, el promedio de la muestra estará mas cerca del promedio del universo. Es por esto que es razonable pensar que el promedio de la muestra es una estimación del promedio del universo.                           DISTRIBUCIONES. NORMAL DOS PARÁMETROS Una distribución muy importante es la Distribución Normal o de Gauss. La ecuación matemática de la función de Gauss es la siguiente: P(x)=12π−−√σ⋅e−(μ−x)22σ2 La distribución normal es una curva con forma de campana, con eje de simetría en el punto correspondiente al promedio del universo μ. La distancia entre el eje de simetría de la campana y el punto de inflexión de la curva es igual a σ, la desviación standard de la población. El área total debajo de la curva es igual a 1. El área debajo de la curva comprendida entre μ - σ y μ + σ es aproximadamente igual a 0,68 del área total; entre μ - 2σ y μ + 2σ es aproximadamente igual a 0,95 del área total: Es importante ver que los únicos parámetros necesarios para dibujar el gráfico de la distribución normal son y (Media y desviación standard de la población). Con estos dos parámetros sabemos donde situar la campana de Gauss (En el punto correspondiente a la media) y cual es su ancho (Determinado por la desviación standard). Cuando nos encontramos con una población de observaciones, si podemos afirmar que la distribución correspondiente es normal, sólo hace falta estimar la media y la desviación standard para tener toda la información necesaria acerca de dicha población.                           DISTRIBUCIONES. T DOS PARÁMETROS  Supongamos dos variables aleatorias independientes, una normal tipificada, Z , y otra con distribución c2 con n grados de libertad, la variable definida según la ecuación: tiene distribución t con n grados de libertad. La función de densidad de la distribución t es: El parámetro de la distribución t es n, su número de grados de libertad. Esta distribución es simétrica respecto al eje Y y sus colas se aproximan asintóticamente al eje X. Es similar a la distribución Z salvo que es platicúrtica y, por tanto, más aplanada. Cuando n tiende a infinito, t tiende asintóticamente a Z y se pueden considerar prácticamente iguales para valores de n mayores o iguales que 30.. Variables T con valores de n progresivamente mayores son cada vez menos platicúrticas Comparación entre la variable T y la normal tipificado.   DISTRIBUCIONES. F. Sean U y V dos variables aleatorias independientes con distribución c2 con n1 y n2 grados de libertad, respectivamente. La variable definida según la ecuación: tiene distribución F con n1, n2 grados de libertad. La función de densidad de la distribución F es: Los parámetros de la variable F son sus grados de libertad n1 y n2. Las distribuciones F tienen una propiedad que se utiliza en la construcción de tablas que es la siguiente: Llamemos fa,n1,n2 al valor de una distribución F con n1 y n2 grados de libertad que cumple la condición, P(F > fa,n1,n2) = α; llamemos f1-a,n1,n2 al valor de una distribución F con n1 y n2 grados de libertad que cumple la condición, P(F > f1-a,n1,n2) = 1- α. Ambos valores están relacionados de modo que uno es el inverso del otro. Variables F con distintos valores de 1,2