ESTIMACIÓN DE PARÁMETROS.
INTRODUCCIÓN
En una población cuya distribución es conocida pero desconocemos algún parámetro, podemos estimar dicho parámetro a partir de una muestra representativa.
Un estimador es un valor que puede calcularse a partir de los datos muestrales y que proporciona información sobre el valor del parámetro. Por ejemplo la media muestral es un estimador de la media poblacional, la proporción observada en la muestra es un estimador de la proporción en la población.
Una estimación es puntual cuando se obtiene un sólo valor para el parámetro. Los estimadores más probables en este caso son los estadísticos obtenidos en la muestra, aunque es necesario cuantificar el riesgo que se asume al considerarlos. Recordemos que la distribución muestral indica la distribución de los valores que tomará el estimador al seleccionar distintas muestras de la población. Las dos medidas fundamentales de esta distribución son la media que indica el valor promedio del estimador y la desviación típica, también denominada error típico de estimación, que indica la desviación promedio que podemos esperar entre el estimador y el valor del parámetro.
Más útil es la estimación por intervalos en la que calculamos dos valores entre los que se encontrará el parámetro, con un nivel de confianza fijado de antemano.
-Llamamos Intervalo de confianza al intervalo que con un cierto nivel de confianza, contiene al parámetro que se está estimando.
-Nivel de confianza es la "probabilidad" de que el intervalo calculado contenga al verdadero valor del parámetro. Se indica por 1-a y habitualmente se da en porcentaje (1-a) 100%. Hablamos de nivel de confianza y no de probabilidad ya que una vez extraída la muestra, el intervalo de confianza contendrá al verdadero valor del parámetro o no, lo que sabemos es que si repitiésemos el proceso con muchas muestras podríamos afirmar que el (1-a) % de los intervalos así construidos contendría al verdadero valor del parámetro.
NECESIDAD DE LA ESTIMACIÓN.
Objetivos: La inferencia estadística se ocupa, entre otras cuestiones, de los procedimientos de estimación de parámetros desconocidos de la distribución de una variable aleatoria o de la población, a partir de la información suministrada por una muestra de tamaño reducido, extraída al azar. La estimación de parámetros por intervalos, permite construir un intervalo que contendrá el parámetro a estimar con una confianza fijada a priori por el experimentador.
El objetivo principal de la estadística inferencial es la estimación, esto es que mediante el estudio de una muestra de una población se quiere generalizar las conclusiones al total de la misma. Como vimos en la sección anterior, los estadísticos varían mucho dentro de sus distribuciones muestrales, y mientras menor sea el error estándar de un estadístico, más cercanos serán unos de otros sus valores
Existen dos tipos de estimaciones para parámetros; puntuales y por intervalo.
Una estimación puntual es un único valor estadístico y se usa para estimar un parámetro. El estadístico usado se denomina estimador.
Una estimación por intervalo es un rango, generalmente de ancho finito, que se espera que contenga el parámetro.
MUESTREO ALEATORIO
Consideremos una población finita, de la que deseamos extraer una muestra. Cuando el proceso de extracción es tal que garantiza a cada uno de los elementos de la población la misma oportunidad de ser incluidos en dicha muestra, denominamos al proceso de selección muestreo aleatorio.
El muestreo aleatorio se puede plantear bajo dos puntos de vista:
- Sin reposición de los elementos;
- Con reposición.
7.4.2.1 Muestreo aleatorio sin reposición
Consideremos una población E formada por N elementos. Si observamos un elemento particular,  , en un muestreo aleatorio sin reposición se da la siguiente circunstancia:
, en un muestreo aleatorio sin reposición se da la siguiente circunstancia:
- La probabilidad de que e sea elegido en primer lugar es
 ;
; - Si no ha sido elegido en primer lugar (lo que ocurre con una probabilidad de
 ), la probabilidad de que sea elegido en el segundo intento es de
), la probabilidad de que sea elegido en el segundo intento es de  .
. - en el (i+1)-ésimo intento, la población consta de N-i elementos, con lo cual si e no ha sido seleccionado previamente, la probabilidad de que lo sea en este momento es de
 .
.
Si consideramos una muestra de  elementos, donde el orden en la elección de los mismos tiene importancia, la probabilidad de elección de una muestra
elementos, donde el orden en la elección de los mismos tiene importancia, la probabilidad de elección de una muestra  cualquiera es
cualquiera es
![\begin{eqnarray*}{{\cal P}}[M] &=& {{\cal P}}[\left( e_1, e_2, \dots, e_n \right...
...N-(n-1)}
\\
&=& \frac{(N-n)!}{N!}
\\
& = & \frac{1}{V_{N,n}}
\end{eqnarray*}](http://www.bioestadistica.uma.es/libro/img1178.gif)
lo que corresponde en el sentido de la definición de probabilidad de Laplace a un caso posible entre las VN,n posibles n-uplas de N elementos de la población.
Si el orden no interviene, la probabilidad de que una muestra
sea elegida es la suma de las probabilidades de elegir una cualquiera de sus n-uplas, tantas veces como permutaciones en el orden de sus elementos sea posible, es decir
![\begin{eqnarray*}{{\cal P}}[M] &=& {{\cal P}}[\left\{ e_1, e_2, \dots, e_n \righ...
...]
\\
& = & \frac{n! \cdot (N-n)!}{N!}
\\
& = & \frac{1}{C_n^N}
\end{eqnarray*}](http://www.bioestadistica.uma.es/libro/img1180.gif)
7.4.2.2 Muestreo aleatorio con reposición
Sobre una población E de tamaño N podemos realizar extracciones de n elementos, pero de modo que cada vez el elemento extraído es repuesto al total de la población. De esta forma un elemento puede ser extraído varias veces. Si el orden en la extracción de la muestra interviene, la probabilidad de una cualquiera de ellas, formada por n elementos es:
Si el orden no interviene, la probabilidad de una muestra cualquiera, será la suma de la anterior, repitiéndola tantas veces como manera de combinar sus elementos sea posible. Es decir,
-

- sea n1 el número de veces que se repite cierto elemento e1 en la muestra;
-

- sea n2 el número de veces que se repite cierto elemento e2;

-

- sea nk el número de veces que se repite cierto elemento ek,
de modo que  . Entonces la probabilidad de obtener la muestra
. Entonces la probabilidad de obtener la muestra

es

es decir,
El muestreo aleatorio con reposición es también denominado muestreo aleatorio simple, que como hemos mencionado se caracteriza por que
- cada elemento de la población tiene la misma probabilidad de ser elegido, y
- las observaciones se realizan con reemplazamiento. De este modo, cada observación es realizada sobre la misma población (no disminuye con las extracciones sucesivas).
Sea X una v.a. definida sobre la población E, y f(x) su ley de probabilidad.

En una muestra aleatoria simple, cada observación tiene la distribución de probabilidad de la población: 
Además todos las observaciones de la v.a. son independientes, es decir
Las relaciones(7.1)-(7.2) caracterizan a las muestras aleatorias simples.
Además todos las observaciones de la v.a. son independientes, es decir
Las relaciones(7.1)-(7.2) caracterizan a las muestras aleatorias simples.
La selección de una muestra aleatoria puede realizarse con la ayuda de #.#>
7.4.2.3 Tablas de números aleatorios: Lotería Nacional
Un ejemplo de una tabla de números aleatorios consiste en la lista de los números de Lotería Nacional premiados a lo largo de su historia, pues se caracterizan por que cada dígito tiene la misma probabilidad de ser elegido, y su elección es independiente de las demás extracciones.
Un modo de hacerlo es el siguiente. Supongamos que tenemos una lista de números aleatorios de k=5 cifras (00000-99.999), una población de N=600individuos, y deseamos extraer una muestra de n=6 de ellos. En este caso ordenamos a toda la población (usando cualquier criterio) de modo que a cada uno de sus elementos le corresponda un número del 1 al 600. En segundo lugar nos dirigimos a la tabla de números aleatorios, y comenzando en cualquier punto extraemos un número t, y tomamos como primer elemento de la muestra al elemento de la población:
El proceso se repite tomando los siguientes números de la tabla de números aleatorios, hasta obtener la muestra de 10 individuos.
Las cantidades
pueden ser consideradas como observaciones de una v.a. U, que sigue una distribución uniforme en el intervalo [0,1]
7.4.2.4 Método de Montecarlo
El método de Montecarlo es una técnica para obtener muestras aleatorias simples de una v.a. X, de la que conocemos su ley de probabilidad (a partir de su función de distribución F). Con este método, el modo de elegir aleatoriamente un valor de X siguiendo usando su ley de probabilidad es:
- 1.
- Usando una tabla de números aleatorios7.1 se toma un valor u de una v.a.
 .
. - 2.
- Si X es continua tomar como observación de X, la cantidad x=F-1(u). En el caso en que X sea discreta se toma x como el percentil
 de X, es decir el valor más pequeño que verifica que
de X, es decir el valor más pequeño que verifica que  .
.
Este proceso se debe repetir n veces para obtener una muestra de tamaño n.
7.4.2.5 Ejemplo
Si queremos extraer n=10 muestras de una distribución  podemos recurrir a una tabla de números aleatorios de k=5cifras, en las que observamos las cantidades (por ejemplo)
podemos recurrir a una tabla de números aleatorios de k=5cifras, en las que observamos las cantidades (por ejemplo)
A partir de ellas podemos obtener una muestra de  usando una tabla de la distribución normal:
usando una tabla de la distribución normal:
| Números aleatorios | Muestra | Muestra |
| ti | xi = F-1(ui) | |
| 76.293 | 0'76 | 0'71 |
| 31.776 | 0'32(=1-0'68) | -0'47 |
| 50.803 | 0'51 | 0'03 |
| 71.153 | 0'71 | 0'55 |
| 20.271 | 0'20(=1-0'80) | -0'84 |
| 33.717 | 0'34(=1-0'66) | -0'41 |
| 17.979 | 0'18(=1-0'82) | -0'92 |
| 52.125 | 0'52 | 0'05 |
| 41.330 | 0'41(=1-0'59) | -0'23 |
| 95.141 | 0'95 | 1'65 |
Obsérvese que como era de esperar, las observaciones xi tienden a agruparse alrededor de la esperanza matemática de  . Por otra parte, esto no implica que el valor medio de la muestra sea necesariamente
. Por otra parte, esto no implica que el valor medio de la muestra sea necesariamente  . Sin embargo como sabemos por el teorema de Fisher que
. Sin embargo como sabemos por el teorema de Fisher que

su dispersión con respecto al valor central es pequeña, lo que implica que probablemente el valor medio  estará muy próximo a 0, como se puede calcular:
estará muy próximo a 0, como se puede calcular:
Obsérvese que si el problema fuese el inverso, donde únicamente conociésemos las observaciones xi y que el mecanismo que generó esos datos hubiese sido una distribución normal de parámetros desconocidos, con  obtenida hubiésemos tenido una buena aproximación del ``parámetro desconocido''
obtenida hubiésemos tenido una buena aproximación del ``parámetro desconocido''  . Sobre esta cuestión volveremos más adelante al abordar el problema de la estimación puntual de parámetros.
. Sobre esta cuestión volveremos más adelante al abordar el problema de la estimación puntual de parámetros.
ALEATORIO SIMPLE
El procedimiento empleado es el siguiente: 1) se asigna un número a cada individuo de la población y 2) a través de algún medio mecánico (bolas dentro de una bolsa, tablas de números aleatorios, números aleatorios generados con una calculadora u ordenador, etc.) se eligen tantos sujetos como sea necesario para completar el tamaño de muestra requerido.
Elegido el tamaño de la muestra, los elementos que la compongan se han de elegir aleatoriamente entre los N de la población. Con calculadora: se utilizan los números aleatorios.
-Se numeran los alumnos del 1 al 20
-Se sortean 30 números entre lo 120
-La muestra estará formada por los 30 alumnos a los que les corresponda los números obtenidos.
También Muestreo aleatorio simple: En una población de tamaño N, cada individuo tiene una probabilidad de ser elegido, de 1/N.
Ejemplo: Se requiere seleccionar 10 estudiantes como muestra del grupo de 250 del programa de sociología.
Hay dos formas:
- Por sorteo: Se escriben los nombres en fichos y luego se sacan 10 fichos al azar de la bolsa.
- Se asigna un número a cada uno y se seleccionan 10 de una tabla de números aleatorios.
SISTEMÁTICO
Se ordenan previamente los individuos de la población; después se elige uno de ellos al azar, a continuación, a intervalos constantes, se eligen todos los demás hasta completar la muestra.
Este procedimiento exige, como el anterior, numerar todos los elementos de la población, pero en lugar de extraer n números aleatorios sólo se extrae uno. Se parte de ese número aleatorio i, que es un número elegido al azar, y los elementos que integran la muestra son los que ocupa los lugares i, i+k, i+2k, i+3k,…,i+(n-1)k, es decir se toman los individuos de k en k, siendo k el resultado de dividir el tamaño de la población entre el tamaño de la muestra: k= N/n. El número i que empleamos como punto de partida será un número al azar entre 1 y k.
Muestreo sistemático: En este caso los elementos se escogen aplicando un criterio de selección pre-establecido y uniforme.
Ejemplo: Se seleccionan dentro de la población (250) a un número de “n” elementos a partir de un intervalo Q= N/n.
Q= 250/10 = 25, Significa que de cada 25 personas será elegida una, hasta completar el listado de 250.
El riesgo este tipo de muestreo está en los casos en que se dan periodicidades en la población ya que al elegir a los miembros de la muestra con una periodicidad constante (k) podemos introducir una homogeneidad que no se da en la población. Imaginemos que estamos seleccionando una muestra sobre listas de 10 individuos en los que los 5 primeros son varones y los 5 últimos mujeres, si empleamos un muestreo aleatorio sistemático con k=10 siempre seleccionaríamos o sólo hombres o sólo mujeres, no podría haber una representación de los dos sexos.
Muestreo estratificado
Consiste en la división previa de la población de estudio en grupos o clases que se suponen homogéneos con respecto a alguna característica de las que se van a estudiar. A cada uno de estos estratos se le asignaría una cuota que determinaría el número de miembros del mismo que compondrán la muestra. Dentro de cada estrato se suele usar la técnica de muestreo sistemático, una de las técnicas de selección más usadas en la práctica.
Según la cantidad de elementos de la muestra que se han de elegir de cada uno de los estratos, existen dos técnicas de muestreo estratificado:
- Asignación proporcional: el tamaño de la muestra dentro de cada estrato es proporcional al tamaño del estrato dentro de la población.
- Asignación óptima: la muestra recogerá más individuos de aquellos estratos que tengan más variabilidad. Para ello es necesario un conocimiento previo de la población.
Por ejemplo, para un estudio de opinión, puede resultar interesante estudiar por separado las opiniones de hombres y mujeres pues se estima que, dentro de cada uno de estos grupos, puede haber cierta homogeneidad. Así, si la población está compuesta de un 55% de mujeres y un 45% de hombres, se tomaría una muestra que contenga también esos mismos porcentajes de hombres y mujeres.
Para una descripción general del muestreo estratificado y los métodos de inferencia asociados con este procedimiento, suponemos que la población está dividida en h subpoblaciones o estratos de tamaños conocidos N1, N2,..., Nh tal que las unidades en cada estrato sean homogéneas respecto a la característica en cuestión. La media y la varianza desconocidas para el i-ésimo estrato son denotadas por mi y si2, respectivamente.
POR CONJUNTO O MÉTODO
Método:
Denominamos población o universo conceptual al conjunto de unidades sobre las que pretendamos obtener cierta información. Esas unidades pueden ser individuales (como, por ejemplo, mujeres de Andalucía, personas de la Tercera Edad, etcétera), compuestas (como, por ejemplo, escuela, ayuntamientos, etcétera), o una serie de objetos (como, por ejemplo, editoriales de un periódico, artículos, etcétera).
Como característica de cualquier población hay que destacar:
· Una correcta delimitación de la misma, de manera que se pueda definir sin problemas si una unidad pertenece o no.
· Que esté constituida por unidades de la misma naturaleza.
En la mayoría de las ocasiones, y debido a la complejidad de la recogida y clasificación de análisis de los datos, es prácticamente imposible que el estudio abarque a todas las unidades que comprendan la población, salvo que ésta sea muy pequeña.
En esos casos se toma una parte representativa de la población, que debe reducir de la forma más exacta posible las características de la población. A esa parte de la población se le llama muestra. Así, pues, una muestra es una parte representativa de la población. Los elementos principales de una muestra son:
· El marco o base de la muestra. Conjunto de unidades que constituyen la población. Por ejemplo, españoles de ambos sexos que viven en la península y son mayores de edad. Lo ideal sería tener un registro de la población en el que aparecieran todas sus unidades, pero hay ocasiones en que ese registro no existe, pues hay poblaciones que no están censadas. En la práctica suelen utilizarse bases ya formadas como los censos de población o los padrones municipales, etcétera.
· Unidades muestrales. Cada uno de los elementos que constituyen la base o marco de la muestra. Esas unidades pueden ser individuales o colectivas. Si la unidad es colectiva, al número de individuos que la componen se le llama talla de la muestra.
· FRACCIÓN DE MUESTREO.- Es el porcentaje que representa la muestra sobre el total de la población (n/N 100).
Ejemplo.-
N = 580.000 (población)
n = 2.000 (muestra) (2.000/580.000) 100= 0'35
· COEFICIENTE DE ELEVACIÓN.- Es el número de veces que el tamaño de la población contiene al tamaño de la muestra (N/n).
Ejemplo.-
N = 200.000 (población)
n = 1.000 (muestra) 200.000/1.000=200
2. Métodos de muestreo.
Existen distintos métodos para obtener muestras:
· PROBABILÍSTICOS.- Si cada elemento de la población tiene una probabilidad, conocida y distinta de 0, de ser elegido dentro de la población, al formar parte de la muestra.
La gran ventaja que presentan las muestras probabilísticas es que permiten la inferencia estadística. Es decir, permiten trasladar los datos de la muestra al conjunto de la población mientras que las no probabilísticas no.
Para que un muestreo sea probabilístico han de seguirse determinadas normas en el proceso de elección de los individuos (o unidades muestrales). Esas normas dan origen a los 4 métodos básicos de muestreo probabilístico. De los 4 métodos, los 3 primeros son monoetápicos, las unidades muestrales se eligen en una sola etapa.
EN DOS ETAPAS
Cuando las poblaciones son muy extensas, o complejas, la simple toma de muestras al azar se transforma en un gran problema, que suele requerir mucho tiempo. El tiempo necesario para obtener una muestra de dimensiones determinadas puede ser muy abreviado mediante el empleo de un muestreo en dos etapas. En primer lugar, el conjunto de la población puede ser dividido en una serie de unidades primarias, o subpoblaciones, varias de las cuales se toman como muestra. Se toma una muestra secundaria, o submuestra, de cada una de estas subpoblaciones, que a su vez son muestras de la población total. Por ejemplo, para estimar la captura total a lo largo de una línea costera, se puede tomar como unidad básica cada desembarco. La medición de una serie de desembarcos tomados al azar a lo largo de la costa requeriría efectuar muchos viajes, imposibles de realizar; la solución consiste en seleccionar (por ejemplo, mediante números al azar) ciertos lugares de desembarco en determinados días, y en estos lugares seleccionar una serie de desembarcos.
Por supuesto, el submuestreo se puede realizar en más de dos etapas. En el ejemplo anterior, podría interesar algún dato, como el estado de madurez, para lo cual se tomaría una caja de pescado (o una parte de la misma), con lo que el muestreo se habría realizado en tres (o cuatro) etapas.
La desventaja de un submuestreo consiste, desde luego, en que los individuos de una misma unidad primaria son probablemente más parecidos entre sí que los del conjunto de la población. De esta manera, después de examinar un individuo de una unidad, tal como el peso de la captura de un barco en un lugar determinado, si se siguen examinando individuos de esa unidad, se obtendrá menos información del conjunto de la población (por ejemplo, la captura media por barco de todos los lugares de desembarco) que si se examinan individuos de otras unidades primarias. El problema consiste en deducir el número más conveniente de muestras que se debe tomar en un tiempo dado al emplear un muestreo en dos etapas. En términos generales, si los individuos dentro de una unidad primaria son muy variables, lo mejor será tomar muchas muestras dentro de cada unidad en, comparativamente, pocas unidades primarias. Por el contrario, si la variación de los individuos es pequeña dentro de cada unidad, pero hay diferencias considerables entre las unidades, entonces deberán someterse a muestreo muchas unidades primarias, con un pequeño número de individuos por muestra en cada una de ellas.
El método puede ser ilustrado en términos matemáticos: supóngase, para mayor sencillez, que la población puede dividirse en K unidades primarias, cada una de Nindividuos, y que están sometidas a muestreo k unidades primarias, tomándose una submuestra de n individuos en cada una.
Si M es la media de la población, y Mi la media de la ia unidad primaria, entonces la estimación de la media de una unidad primaria bajo muestreo será:
donde xij es el valor del j° individuo en la unidad ia y la estimación de la media de la población será
............................(2.4)
La variancia de mi en torno a Mi será 1/n × Sw2, en donde Sw2 es la variancia de los individuos de la ia unidad primaria en torno a la media de la unidad. La variancia de la media estimada para la población constará de dos partes: la variancia de las medias estimadas para las unidades en torno a las medias verdaderas de las unidades, y la variancia de estas últimas en torno a la media de la población; esto es
........................................(2.5)
donde SB2 es la variancia de las medias de las unidades en torno a la media de la población. Una estimación no sesgada de la variancia de m será

.............................(2.6)
Ejemplo 2.4.1
(tomado de Pope, 1956)
Como muestra al azar del desembarco total de arenque en una semana, se toma una serie de desembarcos individuales, y de cada desembarco seleccionado una muestra de 50 arenques, y se miden. Se obtienen los siguientes datos:
Barco
|
1
|
2
|
3
|
4
|
5
|
Suma  |
1 244,3
|
1 324,2
|
1 335,4
|
1 299,7
|
1 270,5
|
Suma de cuadrados  |
31 020,97
|
35 127,08
|
35 730,30
|
33 900,99
|
32 558,55
|
Estímese la longitud media del arenque en los desembarcos de la semana, y su error típico. Primero se obtendrá la media para cada barco, que son 24,9, 26,5, 26,7, 26,0 y 25,4. Por tanto, las estimaciones que se piden se obtendrán por
m2 = 1/5 (24,9 + ... + 25,4) = 25,9
sm=0,34
Las variancias entre y dentro de las unidades primarias pueden también estimarse separadamente. Dentro de cada unidad primaria, se tendrá una estimación de Sw2por
Estas estimaciones por separado en las unidades primarias pueden combinarse por medio de
.............................(2.7)
Según las ecuaciones (2.5) y (2.6) la variancia entre las unidades puede deducirse de la ecuación
.............................(2.8)
Siendo dados los valores de Sw2 por la ecuación (2.7)
Ejemplo 2.4.2
Calcúlese la variancia de la longitud del arenque dentro y entre los barcos, de acuerdo con los datos del Ejemplo 2.4.1. Como estimación de la variancia dentro de los barcos, se tiene que
5 x 49 x Sw2 = (31020,97 - 1/50 x 1244,32) + ... + ...
por tanto
245 Sw2 = 378,62 Sw2 = 1,545
También
SB2 = 0,56 - 0,03 = 0,53
En los cálculos de los ejemplos 2.4.1 y 2.4.2 se ha podido ver que la mayor parte de Sm2, la variancia de la longitud media estimada de todos los peces desembarcados, se debe a SB2 la variancia entre los barcos. De la ecuación (2.5) se deduce que el efecto de esta variancia puede reducirse aumentando k, o sea, el número de unidades primarias bajo muestreo, pero no incrementando n, el número de individuos sometidos a muestreo en cada unidad primaria. Así pues, el tiempo empleado en el muestreo de los desembarcos de arenque podría aprovecharse más eficazmente reduciendo el número de individuos en las muestras y aumentando el número de barcos bajo muestra, por ejemplo, 6 muestras de 30 peces, con un total de 180 peces, en vez de 5 muestras de 50 peces, con un total de 250 peces. La mejor forma de utilizar el tiempo dependerá del que se emplee en cada etapa de muestreo y de la variancia contenida en ellas. El tiempo total empleado se puede dividir aproximadamente en tres partes:
a) el tiempo inicial; el tiempo que se emplea en la preparación, incluyendo el traslado desde el centro de trabajo al área de muestreo. Este tiempo es más o menos constante, independientemente del volumen del muestreo; b) el tiempo entre las unidades primarias; en el ejemplo anterior, el tiempo empleado en ir de un barco a otro, que será proporcional al número de unidades primarias;
c) el tiempo dentro de las unidades primarias; que es el tiempo que se emplea en examinar los individuos en cada unidad primaria. El tiempo total podra ser, por tanto, igual a
t = t0 + k tb + n k tw .............................. (2.9)
t0 = tiempo inicial
tb = tiempo para ir de una unidad primaria a otra
tw = tiempo empleado en examinar un individuo.
La mejor forma de distribuir el tiempo de muestreo (es decir, la que da una variancia mínima), de acuerdo con un número determinado de individuos bajo muestreo en cada unidad primaria, viene dada por
............................(2.10)
Ejemplo 2.4.3
Utilizando los datos de los ejemplos anteriores, y suponiendo que en un minuto se pueden medir 20 peces, y que el tiempo empleado para ir de un barco a otro es de 5 minutos, demuéstrese que la variancia mínima en la longitud media estimada y para una cantidad dada de muestreo es de 17 peces aproximadamente, resultado obtenido con muestras secundarias.
Hasta ahora, se había supuesto que todas las unidades primarias eran del mismo tamaño, pero esto no es lo corriente. Cuando sean desiguales, se hará preciso aplicar un factor de corrección para cada unidad. La ecuación (2.4) puede reescribirse como sigue
..........................(2.11)
donde Ni = número de individuos en la ia unidad primaria
N = S Ni = número total en todas las unidades primarias de muestreo
N = S Ni = número total en todas las unidades primarias de muestreo
o como..................................(2.12)
donde ni es el número de individuos bajo muestra en la ia unidad primaria, que no tiene por qué ser igual en todas ellas. Si se toma ni en cada unidad de tal manera que en todas ellas la razón de muestreo ni/Ni sea la misma para todas las unidades, e igual a p, entonces (2.12) se reduce a
es decir
..........................................(2.13)
donde n es el número total de individuos de la muestra, siendo ésta, desde luego, la forma más conveniente de computación. La fórmula de la variancia (ecuación 2.5) puede también reescribirse así
donde
La fórmula (ecuación 2.10) sobre el mejor número de individuos por muestra en cada unidad no hay que aplicarla de manera estricta. Podría modificarse para que determinara con precisión la mejor muestra en cada unidad primaria. Sin embargo, esta fórmula sería más bien prolija, y necesitaría una información adicional sobre la variancia en cada unidad primaria (que puede no ser igual en todas las unidades). Tanto esfuerzo puede muy bien no merecer la pena, y ser más razonable utilizar la ecuación (2.10), modificada empíricamente, incrementando la muestra en las unidades más grandes o más variables.
Cuando el objetivo del muestreo sea medir alguna cantidad total, como el peso total desembarcado de cierta especie de peces, y no un valor medio, como la longitud media de los peces, el análisis de los resultados, como figura en las ecuaciones (2.11) - (2.13) deberá modificarse. El total en la ia unidad bajo muestreo será
donde Ni/ni es el factor elevador o de ponderación para la ia unidad primaria, y es igual al recíproco de la proporción tomada como muestra. El total en el conjunto de la población viene dado por
donde N = número total de individuos en la población. Si N no es conocido, como bien puede suceder, entonces en vez de N/Ni debe emplearse como factor aproximado elevador K/k, donde K es el número total de unidades primarias y k es el número total de unidades bajo muestreo (si el número de individuos de cada unidad primaria fuera el mismo, los dos factores coincidirían). Es absolutamente indispensable utilizar dos factores elevadores, uno para relacionar la muestra con el conjunto de la unidad primaria, y otro para relacionar las unidades primarias sometidas a muestreo con el conjunto de la población. El empleo de factores ponderadores equivocados puede ocasionar sesgos importantes, si es que hay grandes diferencias en la composición entre las unidades primarias, en especial si están correlacionadas con el número de individuos en la unidad primaria. Supóngase, por ejemplo, que se desea estimar la cantidad total desembarcada en un cierto lugar de una determinada especie de peces que viven predominantemente en fondos costeros. Como unidad primaria se puede tomar la captura de cada barco, utilizando como muestra una caja de pescado de cada barco seleccionado. Es muy probable que los barcos grandes pesquen en fondos más alejados de la costa, que consigan capturas mayores, y que haya en ellas una pequeña proporción de peces costeros. Si a las muestras de estos barcos grandes se les diera el mismo factor ponderador que a las de los más pequeños que actúan junto a la costa, la proporción de especies costeras podría muy bien ser sobreestimada.
Ejemplo 2.4.4
Treinta barcos desembarcaron peces en un lugar determinado. Se tomaron como muestra 10 barcos, de cada uno de los cuales se sometió a muestreo una caja, determinándose el peso de dos de las especies, con los siguientes resultados:
Número del barco
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Número de cajas desembarcadas |
28
|
10
|
16
|
20
|
18
|
12
|
10
|
5
|
15
|
25
|
| Peso de la especie A en 1 caja (kg) |
10
|
1
|
2
|
2
|
7
|
8
|
3
|
2
|
9
|
12
|
| Peso de la especie B en 1 caja (kg) |
1
|
10
|
2
|
2
|
2
|
7
|
3
|
9
|
8
|
2
|
Calcúlese el peso total de los desembarcos de cada especie, (a) utilizando la información anterior, (b) utilizando la información adicional de que el total de desembarcos de todos los barcos fue de 450 cajas. Compárese la proporción de las dos especies en el total de desembarcos, con la proporción en las 10 cajas bajo muestreo (una caja equivale a 50 kg).
NO NECESARIAMENTE IGUALES
En este caso se trata de comparar dos métodos o tratamientos, pero se quiere que las unidades experimentales donde se aplican los tratamientos sean las mismas, ó lo más parecidas posibles, para evitar influencia de otros factores en la comparación.
Este es un procedimiento de estimación para la diferencia de dos medias cuando las muestras son dependientes y las varianzas de las dos poblaciones no necesariamente son iguales.
Las muestras pareadas involucran un procedimiento en el cual varios pares de observaciones se equiparan de la manera más próxima posible, en términos de características relevantes. Los dos grupos de observaciones son diferentes sólo en un aspecto o "tratamiento".
Toda diferencia subsiguiente en los dos grupos se atribuye a dicho tratamiento. Las ventajas de las muestras pareadas son:1) Pueden utilizar muestras muy pequeñas.2) Se encuentran varianzas más pequeñas.3)
Menos grados de libertad se pierden en el análisis.4) Resulta un error de muestreo más pequeño (la variación entre observaciones reduce debido a que corresponden de la forma más próxima posible).
Otro método para utilizar muestras pareadas a diferencia de la situación que se describió cuando las muestras son independientes, las condiciones de las dos poblaciones no designan de forma aleatoria a las unidades experimentales.
Más bien, cada unidad experimental homogénea recibe ambas condiciones poblacionales; como resultado, cada unidad experimental tiene un par de observaciones, una para cada población .Sea el valor de tratamiento I y el valor del tratamiento II en el i-ésimo sujeto.
di =xi-yi
Diferencia de los tratamientos en el i-ésimo sujeto.
DATOS APAREADOS
Los datos apareados son los que tenemos cuando dos muestras con valores pero los datos de cada muestra pertenecen a los mismos individuos, es decir tenemos las medidas de cada variable en la misma persona o individuo, por ejemplo medimos los valores de tensión arterial mínimo y máximo, si sacamos la muestra en el mismo grupo de personas, para cada una de ellas dispondremos de dos valores uno para cada muestra, que están relacionados (apareados) al ser del mismo individuo, por ejemplo hemos medido la tensión máxima y mínima en las 4 personas.
Persona --- mínimo --- máximo
1 --- 110 --- 135
2 --- 90 --- 115
3 --- 101 --- 121
4 ---- 120 --- 150
Es diferente a haber medido la tensión máxima en 4 persona y la mínima en otras 4.
Los datos apareados pueden usarse fácilmente en varias pruebas estadísticas ya que basta crear una variable que mida su diferencia en cada individuo y trabajar con una sola variable en lugar de dos.
Persona --- mínimo --- máximo
1 --- 110 --- 135
2 --- 90 --- 115
3 --- 101 --- 121
4 ---- 120 --- 150
Es diferente a haber medido la tensión máxima en 4 persona y la mínima en otras 4.
Los datos apareados pueden usarse fácilmente en varias pruebas estadísticas ya que basta crear una variable que mida su diferencia en cada individuo y trabajar con una sola variable en lugar de dos.
DE LA RAZÓN DE DESVIACIONES ESTÁNDAR
La desviación estándar o desviación típica (denotada con el símbolo σ o s, dependiendo de la procedencia del conjunto de datos) es una medida de centralización o dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva.
Se define como la raíz cuadrada de la varianza. Junto con este valor, la desviación típica es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de sumedia aritmética, expresada en las mismas unidades que la variable.
Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que presentan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad al momento de describirlos e interpretarlos para la toma de decisiones.
Formulación Muestral
La varianza representa la media aritmética de las desviaciones con respecto a la media que son elevadas al cuadrado.
Si atendemos a la colección completa de datos (la población en su totalidad) obtenemos la varianza poblacional; y si por el contrario prestamos atención sólo a una muestra de la población, obtenemos en su lugar la varianza muestral. Las expresiones de estas medidas son las que aparecen a continuación donde nos explican mejor el texto.
Expresión de la varianza muestral:
Segunda forma de calcular la varianza muestral:
podemos observar que como
 (sumamos n veces 1 y luego dividimos por n)
(sumamos n veces 1 y luego dividimos por n)
y como
obtenemos
Expresión de la varianza poblacional:
donde  es el valor medio de
es el valor medio de 
 es el valor medio de
es el valor medio de 
Expresión de la desviación estándar poblacional:
Por la formulación de la varianza podemos pasar a obtener la desviación estándar, tomando la raíz cuadrada positiva de la varianza. Así, si efectuamos la raíz de la varianza muestral, obtenemos la desviación típica muestral; y si por el contrario, efectuamos la raíz sobre la varianza poblacional, obtendremos la desviación típica poblacional.
Expresión de la desviación estándar muestral:
También puede ser tomada como
con a como  y s como
y s como 
 y s como
y s como 
Además se puede tener una mejor tendencia de medida al desarrollar las fórmulas indicadas pero se tiene que tener en cuenta la media, mediana y moda.
Interpretación y aplicación
La desviación estándar es una medida del grado de dispersión de los datos con respecto al valor promedio. Dicho de otra manera, la desviación estándar es simplemente el "promedio" o variación esperada con respecto a la media aritmética.
Por ejemplo, las tres muestras (0, 0, 14, 14), (0, 6, 8, 14) y (6, 6, 8, 8) cada una tiene una media de 7. Sus desviaciones estándar muestrales son 8,08; 5,77 y 1,15 respectivamente. La tercera muestra tiene una desviación mucho menor que las otras dos porque sus valores están más cerca de 7.
La desviación estándar puede ser interpretada como una medida de incertidumbre. La desviación estándar de un grupo repetido de medidas nos da la precisión de éstas. Cuando se va a determinar si un grupo de medidas está de acuerdo con el modelo teórico, la desviación estándar de esas medidas es de vital importancia: si la media de las medidas está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces consideramos que las medidas contradicen la teoría. Esto es coherente, ya que las mediciones caen fuera del rango de valores en el cual sería razonable esperar que ocurrieran si el modelo teórico fuera correcto. La desviación estándar es uno de tres parámetros de ubicación central; muestra la agrupación de los datos alrededor de un valor central (la media o promedio).
Desglose
La desviación estándar (DS/DE), también llamada desviación típica, es una medida de dispersión usada en estadística que nos dice cuánto tienden a alejarse los valores concretos delpromedio en una distribución. De hecho, específicamente, la desviación estándar es "el promedio del cuadrado de la distancia de cada punto respecto del promedio". Se suele representar por unaS o con la letra sigma,  .
.
 .
.
La desviación estándar de un conjunto de datos es una medida de cuánto se desvían los datos de su media. Esta medida es más estable que el recorrido y toma en consideración el valor de cada dato.
Distribución de probabilidad continua
Es posible calcular la desviación estándar de una variable aleatoria continua como la raíz cuadrada de la integral
donde
Distribución de probabilidad discreta
Así la varianza es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución.
Aunque esta fórmula es correcta, en la práctica interesa realizar inferencias poblacionales, por lo que en el denominador en vez de n, se usa n-1 (Corrección de Bessel) Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción - en este caso una. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la formula desviación estándar muestral. Cuando los casos tomados son iguales al total de la población se aplica la fórmula de desviación estándar poblacional.
También hay otra función más sencilla de realizar y con menos riesgo de tener equivocaciones :
tomado con fines de aclaracion de Frederich Bessel wikipedia ver inglés
Ejemplo
Aquí se muestra cómo calcular la desviación estándar de un conjunto de datos. Los datos representan la edad de los miembros de un grupo de niños: { 4, 1, 11, 13, 2, 7 }
 .
.
En este caso, N = 6 porque hay seis datos:
i = número de datos para sacar desviación estándar
 Sustituyendo N por 6
Sustituyendo N por 6
 Este es el promedio.
Este es el promedio.
2. Calcular la desviación estándar

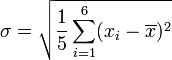 Sustituyendo N - 1 por 5; ( 6 - 1 )
Sustituyendo N - 1 por 5; ( 6 - 1 )
 Sustituyendo
Sustituyendo  por 6,33
por 6,33
 Éste es el valor de la desviación estándar.
Éste es el valor de la desviación estándar.
















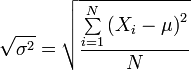


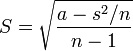


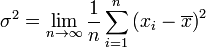










![\sigma = \sqrt{\frac{1}{5} \left [ (4 - 6,33)^2 + (1 - 6,33)^2 + (11 - 6,33)^2 + (13 - 6,33)^2 +(2 - 6,33)^2 + (7 - 6,33)^2 \right ] }](http://upload.wikimedia.org/wikipedia/es/math/0/1/e/01e64c2ef1d79016de1720f766c87a59.png)
![\sigma = \sqrt{\frac{1}{5} \left [ (-2,33)^2 + (-5,33)^2 + 4,67^2 + 6,67^2 + (-4,33)^2 + 0,67^2 \right ] }](http://upload.wikimedia.org/wikipedia/es/math/e/4/1/e416f5431aff08b3ac7dcb8cd4738863.png)



No hay comentarios:
Publicar un comentario