viernes, 20 de julio de 2012

               PRUEBAS DE HIPÓTESIS
Tenemos que empezar por definir que es una hipótesis y que es prueba de hipótesis.
En el análisis estadístico se hace una aseveración, es decir, se plantea una hipótesis, después se hacen las pruebas para verificar la aseveración o para determinar que no es verdadera.
Por tanto, la prueba de hipótesis es un  basado en la evidencia muestral y la teoría de probabilidad; se emplea para determinar si la hipótesis es una afirmación razonable.
Prueba de una hipótesis: se realiza mediante un procedimiento sistemático de cinco paso:
Siguiendo este procedimiento sistemático, al llegar al paso cinco se puede o no rechazar la hipótesis, pero debemos de tener cuidado con esta determinación ya que en la consideración de estadística no proporciona evidencia de que algo sea verdadero. Esta prueba aporta una clase de prueba más allá de una duda razonable.
INTRODUCCIÓN.
Dentro del  de la inferencia estadística, se describe como se puede tomar una muestra aleatoria y a partir de esta muestra estimar el valor de un parámetro poblacional en la cual se puede emplear el método de muestreo y el teorema del valor  lo que permite explicar como a partir de una muestra se puede inferir algo acerca de una población, lo cual nos lleva a definir y elaborar una distribución de muestreo de medias muestrales que nos permite explicar el teorema del limite central y utilizar este teorema para encontrar las probabilidades de obtener las distintas medias maestrales de una población.
Pero es necesario tener conocimiento de ciertos datos de la población como la media, la desviación estándar o la forma de la población, pero a veces no se dispone de esta información.
En este caso es necesario hacer una estimación puntual que es un valor que se usa para estimar un valor poblacional. Pero una estimación puntual es un solo valor y se requiere un intervalo de valores a esto se denomina intervalote confianza y se espera que dentro de este intervalo se encuentre el parámetro poblacional buscado. También se utiliza una estimación mediante un intervalo, el cual es un rango de valores en el que se espera se encuentre el parámetro poblacional
En nuestro caso se desarrolla un procedimiento para probar la validez de una aseveración acerca de un parámetro poblacional este método es denominado Prueba de hipótesis para una muestra.
                       DEFINICIÓN DE HIPÓTESIS.
Hipótesis es una aseveración de una población elaborado con el propósito de poner aprueba, para verificar si la afirmación es razonable se usan datos.
                  HIPÓTESIS NULA Y ALTERNATIVA.

Hipótesis Nula.
En muchos casos formulamos una hipótesis estadística con el único propósito de rechazarla o invalidarla. Así, si queremos decidir si una moneda está trucada, formulamos la hipótesis de que la moneda es buena (o sea p = 0,5, donde p es la probabilidad de cara).
Analógicamente, si deseamos decidir si un procedimiento es mejor que otro, formulamos la hipótesis de que no hay diferencia entre ellos (o sea. Que cualquier diferencia observada se debe simplemente a fluctuaciones en el muestreo de la misma población). Tales hipótesis se suelen llamar hipótesis nula y se denotan por Ho.
Para todo tipo de investigación en la que tenemos dos o más grupos, se establecerá una hipótesis nula.
La hipótesis nula es aquella que nos dice que no existen diferencias significativas entre los grupos.
Por ejemplo, supongamos que un investigador cree que si un grupo de jóvenes se somete a un entrenamiento intensivo de natación, éstos serán mejores nadadores que aquellos que no recibieron entrenamiento. Para demostrar su hipótesis toma al azar una muestra de jóvenes, y también al azar los distribuye en dos grupos: uno que llamaremos experimental, el cual recibirá entrenamiento, y otro que no recibirá entrenamiento alguno, al que llamaremos control. La hipótesis nula señalará que no hay diferencia en el desempeño de la natación entre el grupo de jóvenes que recibió el entrenamiento y el que no lo recibió.
Una hipótesis nula es importante por varias razones:
Es una hipótesis que se acepta o se rechaza según el resultado de la investigación.
El hecho de contar con una hipótesis nula ayuda a determinar si existe una diferencia entre los grupos, si esta diferencia es significativa, y si no se debió al azar.
No toda investigación precisa de formular hipótesis nula. Recordemos que la hipótesis nula es aquella por la cual indicamos que la información a obtener es contraria a la hipótesis de trabajo.
Al formular esta hipótesis, se pretende negar la variable independiente. Es decir, se enuncia que la causa determinada como origen del problema fluctúa, por tanto, debe rechazarse como tal.
Otro ejemplo:
Hipótesis: el aprendizaje de los niños se relaciona directamente con su edad.
Hipótesis Alternativa.
Toda hipótesis que difiere de una dada se llamará una hipótesis alternativa. Por ejemplo: Si una hipótesis es p = 0,5, hipótesis alternativa podrían ser p = 0,7, p " 0,5 ó p > 0,5.
Una hipótesis alternativa a la hipótesis nula se denotará por H1.
  • Al responder a un problema, es muy conveniente proponer otras hipótesis en que aparezcan variables independientes distintas de las primeras que formulamos. Por tanto, para no perder tiempo en búsquedas inútiles, es necesario hallar diferentes hipótesis alternativas como respuesta a un mismo problema y elegir entre ellas cuáles y en qué orden vamos a tratar su comprobación.
HIPÓTESIS SIMPLES Y COMPUESTAS.
Llamaremos hipótesis simples a aquellas que especifican un único valor para el parámetro (por ejemplo m=m0).

Llamaremos hipótesis compuestas a las que especifican un intervalo de valores (por ejemplo: m>m0 ; a< m μ2.
PRUEBAS LATERALES Y UNILATERABLES.



a) Prueba bilateral o de dos extremos: la hipótesis planteada se formula con la igualdad
Ejemplo
H0 : µ = 200
H1 : µ ≠ 200
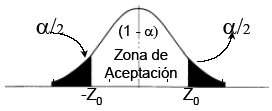
b) Pruebas unilateral o de un extremo: la hipótesis planteada se formula con ≥ o ≤
H0 : µ ≥ 200 H0 : µ ≤ 200
H1 : µ < 200 H1 : µ > 200

En las pruebas de hipótesis para la media (μ), cuando se conoce la desviación estándar (σ) poblacional, o cuando el valor de la muestra es grande (30 o más), el valor estadístico de prueba es z y se determina a partir de:
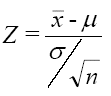
El valor estadístico z, para muestra grande y desviación estándar poblacional desconocida se determina por la ecuación:
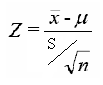
En la prueba para una media poblacional con muestra pequeña y desviación estándar poblacional desconocida se utiliza el valor estadístico t.
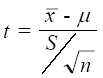
ERRORES TIPO I Y II
Un error tipo I se presenta si la hipótesis nula Ho es rechazada cuando es verdadera y debía ser aceptada. La probabilidad de cometer un error tipo I se denomina con la letra alfa α
Un error tipo II, se denota con la letra griega β se presenta si la hipótesis nula es aceptada cuando de hecho es falsa y debía ser rechazada.
En cualquiera de los dos casos se comete un error al tomar una decisión equivocada.
MATIZ DE DESICIÓN.
Una matriz de decisión es un método cuantitativo, que una empresa puede utilizar para clasificar los factores y seleccionar la mejor oportunidad de entre varias opciones. Este enfoque científico no es necesario que todas las decisiones. Cambios importantes en las operaciones del negocio, sin embargo, pueden llamar a este proceso. Pasos incluyen la definición de la solución y la fijación de prioridades y puntos son asignados, calculados, ponderadas y ascendió. Mediante este método para cada opción examinó los resultados en las puntuaciones totales para todas las opciones, con el puntaje más alto que indica un ideal, una empresa debe elegir.
Una solución ideal es uno que satisfaga o casi satisface todas las necesidades y quiere de una empresa. Propietarios y gerentes tendrán que definir las características que desean en una nueva oportunidad de negocio. La matriz de decisión requiere esto como el primer paso porque el marco para el proceso de decisión restantes comienza aquí. Factores internos y externos pueden influir en la solución ideal, que una empresa busca para completar las operaciones de sus negocio. Este proceso puede tardar más tiempo como propietarios y gerentes deben tener una clara visión para cada opción elegir.
Establecer prioridades con cada opción normalmente implica la configuración de pesos a cada característica de la primera etapa. La matriz de decisión necesita los porcentajes de cada característica para darle una puntuación final de diferentes opciones. Estos pesos pueden ser subjetivos propietarios y administradores pueden colocar figuras como 10, 15 o 25 por ciento junto a cada factor en una opción. Los factores más importantes tienen mayor peso. Todos los pesos porcentaje deben añadir a 100 por ciento para cada opción en la decisión de realizar el proceso.
Dirigentes de la empresa deben asignar puntos como la tercera parte de la matriz de decisión. Una escala básica es de uno a 10, con valores más altos de punto indicando factores más favorables entre diferentes opciones. Cada factor en el resultado de un decisión debe tener una puntuación. Asignar uno como una puntuación debería ser factores que aportan el valor mínimo para el resultado final. El uso de cinco indica que un factor no afecta significativamente el resultado final como la inclusión de factores es promedio.
Con pesos y números asignados, toma de decisiones debe calcular la puntuación de cada posible resultado. Se trata de multiplicar los porcentajes contra los números asignados para cada factor. Una vez completado, el total de todos los resultados es necesario. El resultado es un número que los propietarios y gerentes pueden comparar para todas las opciones. La opción con mayor puntuación representa la mejor oportunidad de la decisión, suponiendo que ningún sesgo existe en el sistema de clasificación de matriz de decisión.
ESTIMACION PUNTUAL.
Estimación puntual: θ= θ0
Se asigna al parámetro  un valor concreto:  λ = 1.25641  (como  λ es la
media de una Poisson, una posible  estimación es la media muestral
X =1 25641 . )
METODOS.
  • Selección de caracteres dignos de ser estudiados.
  • Mediante encuesta o medición, obtención del valor de cada individuo en los caracteres seleccionados.
  • Elaboración de tablas de frecuencias, mediante la adecuada clasificación de los individuos dentro de cada carácter.
  • Representación gráfica de los resultados (elaboración de gráficas estadísticas).
  • Obtención de parámetros estadísticos, números que sintetizan los aspectos más relevantes de una distribución estadística.
MAXIMA VEROSIMILITUD.

En estadística, la estimación por máxima verosimilitud (conocida también como EMV y, en ocasiones, MLE por sus siglas en inglés) es un método habitual para ajustar un modelo y encontrar sus parámetros.
Supóngase que se tiene una muestra x1, x2, …, xn de n observaciones independientes extraídas de una función de distribución desconocida con función de densidad (o función de probabilidad)f0(·). Se sabe, sin embargo, que f0 pertenece a una familia de distribuciones { f(·|θ), θ ∈ Θ }, llamada modelo paramétrico, de manera que f0 corresponde a θ = θ0, que es el verdadero valor del parámetro. 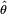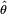Se desea encontrar el valor \scriptstyle\hat\theta (o estimador) que esté lo más próximo posible al verdadero valor θ0.
Tanto xi como θ pueden ser vectores.
La idea de este método es el de encontrar primero la función de densidad conjunta de todas las observaciones, que bajo condiciones de independencia, es
f(x_1,x_2,\ldots,x_n\;|\;\theta) = f(x_1|\theta)\cdot f(x_2|\theta)\cdots f(x_n|\theta)\,
Observando esta función bajo un ángulo ligeramente distinto, se puede suponer que los valores observados x1, x2, …, xn son fijos mientras que θ puede variar libremente. Esta es la función de verosimilitud:
\mathcal{L}(\theta\,|\,x_1,\ldots,x_n) = \prod_{i=1}^n f(x_i|\theta).
En la práctica, se suele utilizar el logaritmo de esta función:
\hat\ell(\theta\,|\,x_1,\ldots,x_n) = \frac1n\ln\mathcal{L} = \frac1n \sum_{i=1}^n \ln f(x_i|\theta).
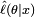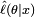El método de la máxima verosimilitud estima θ0 buscando el valor de θ que maximiza \scriptstyle\hat\ell(\theta|x). Este es el llamado estimador de máxima verosimilitud (MLE) de θ0:
\hat\theta_\mathrm{mle} = \underset{\theta\in\Theta}{\operatorname{arg\,max}}\ \hat\ell(\theta\,|\,x_1,\ldots,x_n).
En ocasiones este estimador es una función explícita de los datos observados x1, …, xn, pero muchas veces hay que recurrir a optimizaciones numéricas. También puede ocurrir que el máximo no sea único o no exista.
En la exposición anterior se ha asumido la independencia de las observaciones, pero no es un requisito necesario: basta con poder construir la función de probabilidad conjunta de los datos para poder aplicar el método. Un contexto en el que esto es habitual es el del análisis de series temporales.
    MOMENTOS.
    Con las mismas notaciones usadas a la media y varianza muestral se define el estadístico momento muestral no centrado como:
    m_{k} = M_k(X_1,X_2,...,X_n) = \frac{1}{n} \sum_{i=1}^n X_i^k
    Nótese que m1 es precisamente la media muestral. Análogamente se define el estadístico momento muestral centrado como:
    a_{k} = M_k^c(X_1,X_2,...,X_n) = \frac{1}{n} \sum_{i=1}^n (X_i-\bar{X}_n)^k
    que guarda las siguientes relaciones con estadísticos previamente definidos:
    a_1 = 0 \qquad a_2 = m_2 -m_1^2 = \frac{n-1}{n}S_n^2
PROPIEDADES.
La suma del producto de una constante por una variable, es igual a k veces la sumatoria de la variable.
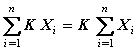
sumatoria
La sumatoria hasta N de una constante, es igual a N veces la constante.
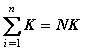
sumatoria
La sumatoria de una suma es igual a la suma de las sumatorias de cada término.
sumatoria
La sumatoria de un producto no es igual al producto de las sumatorias de cada término.
sumatoria
La sumatoria de los cuadrados de los valores de una variable no es igual a la sumatoria de la variable elevado al cuadrado.
sumatoria

ISESGADO Y CONSISTENCIA.
Conviene que los estadísticos, en su función de estimadores de los correspondientes parámetros, reúnan determinados requisitos. Fundamentalmente son:
a)CARENCIA DE SESGO.
Un estimador (estadístico) carece de sesgo si el promedio (media) de todos los valores posibles de todas las muestras posibles de tamaño n de una población es igual al parámetro, es decir, si la media de la distribución muestral del estadístico considerado es igual al valor del parámetro. Así, la media es un estimador insesgado de μ porque se puede demostrar que la media aritmética de una distribución muestral coincide con el valor del parámetro, algo que no puede decirse, por ejemplo, o de la varianza o de la mediana de una población no distribuida normalmente.
b) CONSISTENCIA.
Un estimador es consistente en la medida en que, al aumentar el tamaño de la muestra, (n) su valor se acerca cada vez más al parámetro correspondiente o lo que es lo mismo, si a medida que aumenta el tamaño de la muestra, las estimaciones que ésta proporciona son cada vez más próximas al valor del parámetro.
Algunos estimadores sesgados son consistentes, acercándose cada vez más sus valores a los de sus respectivos parámetros a medida que el tamaño de la muestra (n) aumenta, tal es el caso de s o s2 que son estimadores sesgados pero consistentes de la desviación típica (σ) o de la varianza (σ2) de la población.
ESTIMACION POR INTERVALOS DE CONFIANZA.
Sea desconocida la media poblacional de una cierta variable que deseamos estudiar, sacamos una muestra y se trata de obtener un intervalo (L1,L2) de forma que tengamos una probabilidad alta (1-alfa)% de que la media poblacional esté en ese intervalo. El nivel de confianza del intervalo (1-alfa)% lo fijamos nosotros., se suele trabajar con 95% y a veces con 99% o el 90%; es decir, con probabilidad 0.05, 0.01 o 0.1.
Si se cumple una de las siguientes hipótesis:
  • El tamaño de la muestra es mayor de 30 y la variable sigue un modelo normal.
  • El tamaño de la muestra es mayor de 100.
El intervalo de confianza para la media poblacional es:
Donde z es el valor que en la distribución N(0,1) deja a su derecha un área de alfa/2,  es la media en la muestra, s la cuasidesviación típica (raíz cuadrada de la cuasivarianza) o la desviación típica y n el tamaño de la muestra.
Actividad 15. A una muestra de 150 estudiantes de 2º de Bachillerato n cierta ciudad correspondió una estatura media de 1,73 m, siendo la desviación típica de 4,95 cm. Estima la estatura media de la población, y calcula, para un nivel de confianza del 99%, el intervalo de confianza para la media.
En primer lugar comprueba se cumplen las hipótesis, calcula el valor de alfa y en la tabla de la N(0,1) encuentra el valor de z que deja a su derecha un área de alfa/2. Anótalo en el cuaderno de trabajo.
A continuación introduce los datos en la escena siguiente y se calculará el intervalo de confianza. Cambia la escala si el gráfico no se ve correctamente.
Observando el intervalo podemos apreciar cual será el error máximo cometido. ¿Cuál es? Escribe la fórmula del error máximo cometido.
    
Por tanto podemos estimar la estatura media de la población, con un nivel de confianza del 99%, en 1,73 cm, con un error máximo de 1.04. 
Actividad 16. Se considera los siguientes tiempos de reacción de un producto químico en segundos:
tiempos medios de reacción
1.41.21.31.52.2
frecuencia
6938
6
Obtener un intervalo de confianza del 90% para el tiempo medio de reacción suponiendo que la variable es normal.
Utiliza la primera escena para calcular la media y la desviación típica, recuerda que es la raíz cuadrada de la varianza, después utiliza la escena anterior par calcular el intervalo de confianza.
ESTIMACIÓN POR INTERVALOS DE CONFIANZA PARA LA PROPORCIÓN
Sea p desconocida la proporción de elementos en la población pertenecientes a una categoría C, sacamos una muestra y  se trata de obtener un intervalo (L1,L2) de forma que tengamos una probabilidad alta (1-alfa)% de que la proporción esté en ese intervalo. 
Si se cumple una de las siguientes hipótesis, y que habrá de comprobarlas en todos los problemas son:
En estas condiciones se obtienen los siguientes intervalos según el tamaño de la muestra:
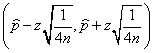
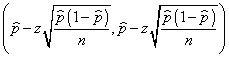
  • El tamaño de la muestra es mayor de 30 y menor o igual de 100.
  • El tamaño de la muestra es mayor de 100.
Donde  , z es el valor que en la distribución N(0,1) deja a su derecha un área de alfa/2, n el tamaño de la muestra.
Actividad 17. En cierta población se seleccionó aleatoriamente una muestra de 300 personas a las que se les sometió a cierto test cultural. De ellas, 225 resultaron aprobadas. Teniendo en cuenta esta información, estimar el porcentaje de persona de esa población que resultarían aprobada si se las sometiera a dicho test cultural. Obtener, con un nivel de confianza del 95%, un intervalo de confianza para la proporción.
Primero calcula, utilizando la escena segunda, cual es el valor de la proporción en la muestra.
Después calcula el valor de alfa y en la tabla de la N(0,1) encuentra el valor de z que deja a su derecha un área de alfa/2. 
PROCEDIMIENTOS DE PRUEBA DE HIPOTESIS.
El jefe de la Biblioteca Especializada de la Facultad de Ingeniería Eléctrica y Electrónica de la UNAC manifiesta que el número promedio de lectores por día es de 350. Para confirmar o no este supuesto se controla la cantidad de lectores que utilizaron la biblioteca durante 30 días. Se considera el nivel de significancia de 0.05
Datos:
Día
Usuarios
Día
Usuarios
Día
Usuario
1
356
11
305
21
429
2
427
12
413
22
376
3
387
13
391
23
328
4
510
14
380
24
411
5
288
15
382
25
397
6
290
16
389
26
365
7
320
17
405
27
405
8
350
18
293
28
369
9
403
19
276
29
429
10
329
20
417
30
364
Solución: Se trata de un problema con una media poblacional: muestra grande y desviación estándar poblacional desconocida.
Paso 01: Seleccionamos la hipótesis nula y la hipótesis alternativa
Ho: μ═350
Ha: μ≠ 350
Paso 02: Nivel de confianza o significancia 95%
α═0.05
Paso 03: Calculamos o determinamos el valor estadístico de prueba
De los datos determinamos: que el estadístico de prueba es t, debido a que el numero de muestras es igual a 30, conocemos la media de la población, pero la desviación estándar de la población es desconocida, en este caso determinamos la desviación estándar de la muestra y la utilizamos en la formula reemplazando a la desviación estándar de la población.
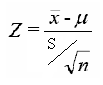
Calculamos la desviación estándar muestral y la media de la muestra empleando Excel, lo cual se muestra en el cuadro que sigue.
Columna1
Media
372.8
Error típico
9.56951578
Mediana
381
Moda
405
Desviación estándar
52.4143965
Varianza de la muestra
2747.26897
Curtosis
0.36687081
Coeficiente de asimetría
0.04706877
Rango
234
Mínimo
276
Máximo
510
Suma
11184
Cuenta
30
Nivel de confianza (95.0%)
19.571868
Paso 04: Formulación de la regla de decisión.
La regla de decisión la formulamos teniendo en cuenta que esta es una prueba de dos colas, la mitad de 0.05, es decir 0.025, esta en cada cola. el área en la que no se rechaza Ho esta entre las dos colas, es por consiguiente 0.95. El valor critico para 0.05 da un valor de Zc = 1.96.
Por consiguiente la regla de decisión: es rechazar la hipótesis nula y aceptar la hipótesis alternativa, si el valor Z calculado no queda en la región comprendida entre -1.96 y +1.96. En caso contrario no se rechaza la hipótesis nula si Z queda entre -1.96 y +1.96.
Paso 05: Toma de decisión.
En este ultimo paso comparamos el estadístico de prueba calculado mediante el Software Minitab que es igual a Z = 2.38 y lo comparamos con el valor critico de Zc = 1.96. Como el estadístico de prueba calculado cae a la derecha del valor critico de Z, se rechaza Ho. Por tanto no se confirma el supuesto del Jefe de la Biblioteca.

 Procedimiento de prueba de hipótesis 2 parámetros.
- Pruebas paramétricas.

PRUEBAS DE HIPÓTESIS DE LAS VARIANCIAS DE DOS POBLACIONES NORMALES
Cuando se trata de comparar las variancias se utiliza la variable F=S²1/S²2, que como se sabe está relacionada con la distribución F con (n1-1, n2-1) grados de libertad.
Se recomienda colocar siempre en el numerador la variancia muestral asociada a la variancia poblacional mayor estos es,
  1. Si H1: s ²1 > s ²2 Þ La estadística de prueba se toma como F=S²1/S²2 .
  2. Si H1: s ²2 > s ²1 Þ La estadística de prueba se toma como F=S²2/S²1.
  3. Si H1: s ²1 ¹ s ²2 Þ La estadística de prueba se toma de tal manera que la mayor de las variancias muestrales aparezca en el numerador.
Las tablas de la distribución F generalmente proporcionan los puntos de la cola superior de la distribución F así que para encontrar valor de la cola inferior, debe utilizarse
, donde f es el valor tabulado de F
Ejemplo 1: Se comparó la eficacia de dos tipos de aceites para evitar el desgaste en ciertas piezas sometidas a intenso trabajo. En trece piezas se utilizó el aceite 1 y en otras trece el aceite 2. Las variancias muestrales fueron S²1 = 64, S²2 = 16. Se desea verificar la hipótesis nula según la cual las variancias de las dos poblaciones son iguales. (a = 0,05)
H0: s ²1 = s ²2
H1: s ²1 ¹ s ²2
n1 = n2 = 13, a = 0,05


Como el valor calculado de F =4 supera el valor tabulado de la cola superior de la distribución, no puede concluirse, al nivel del 5% que las variancias sean iguales.
Siguiendo el criterio de colocar en el numerador siempre la variancia mayor, es suficiente considerar el valor tabulado de la zona derecha de la distribución F.
CONTRASTE DE HIPÓTESIS REFERENTE A DOS MEDIAS POBLACIONALES: MUESTRAS INDEPENDIENTES
Ä Los desvíos de las poblaciones son conocidos
Los supuestos que se deben cumplir son que las medias poblacionales m 1 y m 2 son normales, los desvíos poblacionales y conocidos y las muestras, independientes, de tamaño n1 y n2 respectivamente, estableciendo las siguientes hipótesis:
H0 ) m 1 -m 2 = 0 ó m 1 = m 2
a ) H1 ) m 1 m 2
b) H1 ) m 1 > m 2
c) H1 ) m 1 < m 2
= 0,05
En cualquiera de estos casos el test estadístico que se utiliza es

que se distribuye como una N ( 0,1).
Si y son iguales, lo que equivale a decir que hay una sola variancia, la fórmula anterior se puede reemplazar por la siguiente:

En el contraste a) valores grandes y pequeños de( )y por lo tanto pequeños de Z son suficientes para confirmar H1. Por lo tanto para un ensayo bilateral con nivel de significación , la hipótesis H0 se rechaza si :
Z < ó Z >
En el contraste b) sólo valores grandes de ( ) y de Z confirman la hipótesis H1. En un ensayo unilateral, rechazamos H0 cuando:
Z > Z 1 -
En el contraste c) valores pequeños de la diferencias de medias muestrales y por lo tanto valores pequeños de Z confirman H1 y rechazamos H0 cuando:
Z < Z
Ejemplo 2: El porcentaje de calcio de dos muestras de soja se determinó por dos métodos de mineralización: (A) cenizas secas y (B) mineralización húmeda. Los datos obtenidos fueron:
(A): 0,32 3,32 0,36 0,29 0,27 0,29 0,28
(B): 0,35 0,35 0,34 0,36 0,31 0,28 0,28
Se sabe, por experiencias anteriores que s 1 = s 1 = 0,03. Se desea verificar si ambos métodos producen los mismos resultados. (a = 0,05).
H0 ) m A = m B ó m A -m B = 0
H1 ) m A m B

Por ser un test bilateral, los valores críticos de la distribución normal, para a = 0,05 son –1,96 y 1,96. Como el valor de la estadística calculada cae entre los valores críticos, no hay evidencias como para rechazar la hipótesis nula. Por lo tanto las media de los dos metodos de mineralización no difieren.
Ä Los desvíos de las poblaciones son desconocidos:
a) Se suponen iguales ( ):
Los supuestos que se deben cumplir son: datos extraídos de dos muestras aleatorias independientes de tamaño n1 y n2 respectivamente, cuyas poblaciones son normales con medias poblacionales m 1 y m 2. Las variancias poblacionales no se conocen y se supone que son iguales. Primero se debería docimar la igualdad de dichas varianzas, en particular si los tamaños de las muestras son distintos, a través de la prueba de F de Snedecor. Si son estadísticamente iguales, aplicamos el siguiente test estadístico:

donde
que se distribuye aproximadamente como una t de Student con n1 + n2 -2 grados de libertad. (tn1 + n2 - 2)
Ejemplo 3: Dieciocho plantas de una misma variedad de naranjos fueron tratadas con fertilizantes. A nueve de ellas se les aplico una cierta dosis de nitrógeno (N) y al resto una de nitrógeno y fósforo (NP). Se midió el rendimiento en Kg. por planta; los resultados obtenidos fueron:
_
N: X = 28 kg S² = 9
_
NP: X = 21 kg S² = 7
Interesa conocer si existen diferencias significativas entre los rendimientos de las plantas tratadas con los dos tipos de fertilizante. (a = 0,01).
H0 ) m N = m NP ó m N -m NP = 0
H1 ) m N m NP
Suponiendo que las variancias poblacionales son iguales, de las cuales S²N y S²NP son estimaciones, se calcula la variancia amalgmada. Si el supuesto no fuera válido debería verificarse primeramente la homogneidad de varinacia a través del test F, en particular si las muestras de las poblaciones no son iguales.
Donde

El valor tabulado de t, para 16 grados de libertad y nivel de significación del 1% es igual a ± 2,921. Como el valor de la estadística calculada supera al valor tabulado, se rechas H0 . Conclusión existen diferencias estadísticamente significativas entre los tratamientos, siendo superior el promedio por planta de naranjo, de aquellas que reciben el tratamiento NP.
b) se suponen distintos ( )
Los supuestos son los mismos, pero el test estadístico es:

estadística que se distribuye aproximadamente como una t de Student con grados de libertad que se obtienen mediante la fórmula de Satterwitte:

Gráficamente podemos representar la zona de aceptación y rechazo en la distribución t

si t < -t t > t si t < -t ó t > t
Se rechaza H0 Se rechaza H0 Se rechaza H0
CONTRASTE DE HIPÓTESIS REFERENTE A DOS MEDIAS POBLACIONALES: MUESTRAS APAREADAS
Esta estrategia de la investigacióm surge cuando cada observación para un tratamiento está apareada con otra observación para el otro tratamiento. Este par está compuesto por las mismas unidades experimentales observadas dos veces en distintos momentos de la investigación, o por unidades semejantes.
El procedimeinto consiste en buscar pares de unidades experimentales con características similares y asignar aleatoriamente cada unidad del par a cada uno de los dos tratamientos en estudio. Por ejemplo parejas de gemelos pueden ser asignadas al azar para que reciban dos tratamientos, de tal manera que los miembros de una sola pareja, reciban tratamientos distintos. Pueden así mismo ensayarse dos raciones distintas en dos lotes de terneros formando pares de raza de la misma edad, sexo, etc. y ocurrir que al cabo de un tiempo , exista diferencia significativa o no, entre los promedios de ganancia de peso de ambos lotes, (se elimina la influencia diferencia de calidad entre los lotes).
También puede ocurrir que al estudiar en dos lotes de plantas homogéneas de a pares, la aplicación de herbicidas (uno en cada lote), para ciertas plagas (se obtenga diferencias de resistencia entre los lotes de plantas).
La hipótesis planteada es:
H0 ) ó H0) ó H0)
H1 ) H1) > 0 H1) < 0
= 0,05
Como se establece una hipotesis de un único parámetro poblaciona (se podría pensar en una sola muestra) , el número de grados de liberatd es (n - 1) el test estadístico es:

donde

luego se compara el tc con tn -1 . Las reglas de decisión son:
No se rechaza H0 cuando -t < t < t
Rechazar H0 si t < -t ó t > t
Ejemplo 4: La siguiente tabla muestra los niveles de colesterol en suero para 12 individuos , al principio del programa (ANTES) y al final del mismo (DESPUES).
INDIVIDUO
ANTES XI
DESPUES YI
di
di2
1
2
3
4
5
6
7
8
9
10
11
12
201
231
221
260
228
237
226
235
210
267
284
201
200
236
216
233
224
216
296
195
207
247
210
209
- 1
+ 5
- 5
- 27
- 4
- 21
- 30
- 40
- 33
- 20
- 74
+ 8
1
25
25
625
16
441
900
1600
1089
400
5176
64
TOTAL


-242
10.766
La pregunta que se plantea es: ¿proporcionan los datos suficiente evidencia cómo para concluir que el programa es efectivo en la reducción de los niveles de colesterol en suero?
Aplicar un test de hipótesis para llegar a una decisión al repecto, utilizando un del 0,05.
Las hipótesis planteadas son:
H0)
H1) < 0
 = 0,05


t (11; 0,05) = - 1,7959 (valor de tabla)
Se rechaza H0 ya que -3,02 es menor que -1,7959
Conclusión: Se rechaza la hipótesis nula, existen diferencias altamente significativas entre ANTES y DESPUES. El programa es efectivo.

PRUEBA DE HIPÓTESIS REFERENTE A DOS PROPORCIONES POBLACIONALES
Sean y las proporciones muestrales de dos grandes muestras de tamaños n1 y n2 extraídas de poblaciones que tienen proporciones P1 y P2 respectivamente. Considérese la H0 de que no hay diferencias entre los parámetros poblacionales, es decir:
H0 : P1 = P2, implica que (P1 – P2) = 0
H1: P1 ¹ P2
Una estimación de la proporción poblacional se puede obtener como:

La distribución muestral de la diferencia de proporciones se distribuye aproximadamente normal con media y variancia dadas por:
m p1-p2 = 0 s ²p1-p2 = pq(1/n1+1/n2) (los p de los subíndice tienen sombrero)
y
Por lo tanto la estadística de prueba esta dada por:
~ N(0, 1)
Ejemplo 5: Sobre parcelas sembradas con dos variedades distintas de maíz (A y B), se aplicó un herbicida que resultó ser nocivo en el sentido que destruyó gran parte de las plantas. De un total de 500 plantas de la primera variedad fueron destruidas 200 y de 570 plantas de la segunda variedad, murieron también 200. ¿Se puede considerar que el herbicida es igualmente nocivo para las dos variedades?. (a = 0,05).
H0 : PA = PB, implica que (PA – PB) = 0 H1: PA ¹ PB


Por ser una prueba bilateral, los valores críticos de la distribución normal son –1,96 y 1,96 (a =0,05), como el valor de Z = 1,l8 cae entre estos valores, no se rechaza la hipótesis nula.
Conclusión: Se puede considerar que el herbicida es igualmente nocivo para las dos variedades.

 


- Pruebas no paramétricas.

INTRODUCCIÓN A LA ESTADÍSTICA NO PARAMÉTRICA.
Las pruebas de hipótesis hacen inferencias respecto a los parámetros de la población, como la media. Estas pruebas paramétricas utilizan la estadística paramétrica de muestras que provinieron de la población que se está probando. Para formular estas pruebas, hicimos suposiciones restrictivas sobre las poblaciones de las que extraíamos las muestras. Por ejemplo: suponíamos que las muestras eran grandes o que provenían de poblaciones normalmente distribuidas. Pero las poblaciones no siempre son normales.
Los estadísticos han desarrollado técnicas útiles que no hacen suposiciones restrictivas respecto a la forma de las distribuciones de las poblaciones. Éstas se conocen como pruebas sin distribución, o pruebas no paramétricas. Las hipótesis de una probabilidad no paramétrica se refieren a algo distinto del valor de un parámetro de población
Ventajas de los métodos no paramétricos.
  1. No requieren que hagamos la suposición de que una población está distribuida en forma de curva normal u otra forma específica.
  2. Generalmente, son más fáciles de efectuar y comprender.
  3. Algunas veces, ni siquiera se requiere el ordenamiento o clasificación formal.
Desventajas de los métodos no paramétricos.
  1. Ignoran una cierta cantidad de información
  2. A menudo, no son tan eficientes como las pruebas paramétricas. Cuando usamos pruebas no paramétricas, efectuamos un trueque: perdemos agudeza al estimar intervalos, pero ganamos la habilidad de usar menos información y calcular más rápidamente.

Se denominan pruebas no paramétricas aquellas que no presuponen una distribución de probabilidad para los datos, por ello se conocen también como de distribución libre (distribution free). En la mayor parte de ellas los resultados estadísticos se derivan únicamente a partir de procedimientos de ordenación y recuento, por lo que su base lógica es de fácil comprensión. Cuando trabajamos con muestras pequeñas (n < 10) en las que se desconoce si es válido suponer la normalidad de los datos, conviene utilizar pruebas no paramétricas, al menos para corroborar los resultados obtenidos a partir de la utilización de la teoría basada en la normal.
En estos casos se emplea como parámetro de centralización la mediana, que es aquel punto para el que el valor de X está el 50% de las veces por debajo y el 50% por encima.
Vamos a comentar la filosofía de alguna de las pruebas no paramétricas y en los enlaces se puede aumentar esta información.
  Prueba de Wilcoxon de los rangos con signo
Esta prueba nos permite comparar nuestros datos con una mediana teórica (por ejemplo un valor publicado en un artículo).
Llamemos M0 a la mediana frente a la que vamos a contrastar nuestros datos, y sea X1, X2 .. Xn los valores observados. Se calcula las diferencias X1-M0, X2-M0, ..., Xn-M0. Si la hipótesis nula fuera cierta estas diferencias se distribuirían de forma simétrica en torno a cero.
Para efectuar esta prueba se calculan las diferencias en valor absoluto |Xi-M0| y se ordenan de menor a mayor, asignándoles su rango (número de orden). Si hubiera dos o más diferencias con igual valor (empates), se les asigna el rango medio (es decir que si tenemos un empate en las posiciones 2 y 3 se les asigna el valor 2.5 a ambas). Ahora calculamos R+ la suma de todos los rangos de las diferencias positivas, aquellas en las que Xi es mayor que M0 y R- la suma de todos los rangos correspondientes a las diferencias negativas. Si la hipótesis nula es cierta ambos estadísticos deberán ser parecidos, mientras que si nuestros datos tienen a ser más altos que la mediana M0, se reflejará en un valor mayor de R+, y al contrario si son más bajos. Se trata de contrastar si la menor de las sumas de rangos es excesivamente pequeña para ser atribuida al azar, o, lo que es equivalente, si la mayor de las dos sumas de rangos es excesivamente grande.
 Prueba de Wilcoxon para contrastar datos pareados
El mismo razonamiento lo podemos aplicar cuando tenemos una muestra de parejas de valores, por ejemplo antes y después del tratamiento, que podemos denominar (X1,Y1), (X2,Y2), ... ,(Xn,Yn). De la misma forma, ahora calcularemos las diferencias X1-Y1, X2-Y2, ... , Xn-Yn y las ordenaremos en valor absoluto, asignándoles el rango correspondiente. Calculamos R+ la suma de rangos positivos (cuando Xi es mayor que Yi), y la suma de rangos negativos R-. Ahora la hipótesis nula es que esas diferencias proceden de una distribución simétrica en torno a cero y si fuera cierta los valores de R+ y R- serán parecidos.
  Prueba de Mann-Whitney para muestras independientes
Si tenemos dos series de valores de una variable continua obtenidas en dos muestras independientes: X1, X2, ... , Xn, Y1, Y2, ... , Ym, procederemos a ordenar conjuntamente todos los valores en sentido creciente, asignándoles su rango, corrigiendo con el rango medio los empates. Calculamos luego la suma de rangos para las observaciones de la primera muestra Sx, y la suma de rangos de la segunda muestra Sy. Si los valores de la población de la que se extrajo la muestra aleatoria de X se localizan por debajo de los valores de Y, entonces la muestra de X tendrá probablemente rangos más bajos, lo que se reflejará en un valor menor de Sx del teóricamente probable. Si la menor de las sumas de rangos es excesivamente baja, muy improbable en el caso de que fuera cierta la hipótesis nula, ésta será rechazada.

Publicado por en

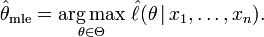
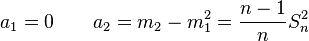
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)